Die Dichtebestimmung von Gold und Silber nach dem Prinzip von Archimedes um die Edelmetalle auf Echtheit zu prüfen soll hier kurz beschrieben werden. Nach diesem Verfahren lässt sich das Volumen und damit auch die Dichte von beliebig geformten Edelmetallformkörpern bestimmen. Man benutzt dabei den Auftrieb, den der Formkörper erfährt, wenn er vollständig in eine Flüssigkeit eingetaucht wird. Grundsätzlich könnte man jede Flüssigkeit verwenden, aber Wasser hat den entscheidenden Vorteil, dass es die Dichte 1g/qcm bzw. 1kg/qdm hat und damit stimmt die Maßzahl des Volumens mit der Maßzahl der Masse überein.
Hinweis: Im allgemeinen Sprachgebrauch werden oft die Begriffe Masse und Gewicht fälschlich gebraucht. Man sagt z.B. die Münze hat ein „Gewicht von 31,1g“ und meint damit – physikalisch richtig – dass sie eine Masse von 31,1g hat. Das Gewicht G ergibt sich, wenn man die Masse mit der ortsabhängigen Fallbeschleunigung (=Ortsfaktor) g multipliziert, also G=m·g. Damit hat eine Masse von 31,1g am Normort ein Gewicht von 305,09 N (Newton). Ein kleines Beispiel mag den Unterschied von Masse und Gewicht verdeutlichen: Wenn ein Raumfahrer in einem um die Erde kreisenden Raumschiff einen Körper mit der Masse 1kg Massestück in die Hand nimmt, so hat es kein Gewicht, weil die Fallbeschleunigung im Orbit den Wert 0 hat. Wenn er aber diesen Körper auf die gleiche Geschwindigkeit beschleunigen will wie auf der Erdoberfläche, so muss er dazu die gleiche Kraft aufwenden. Kurz: Die Masse ist – im Gegensatz zum Gewicht – ortsunabhängig!
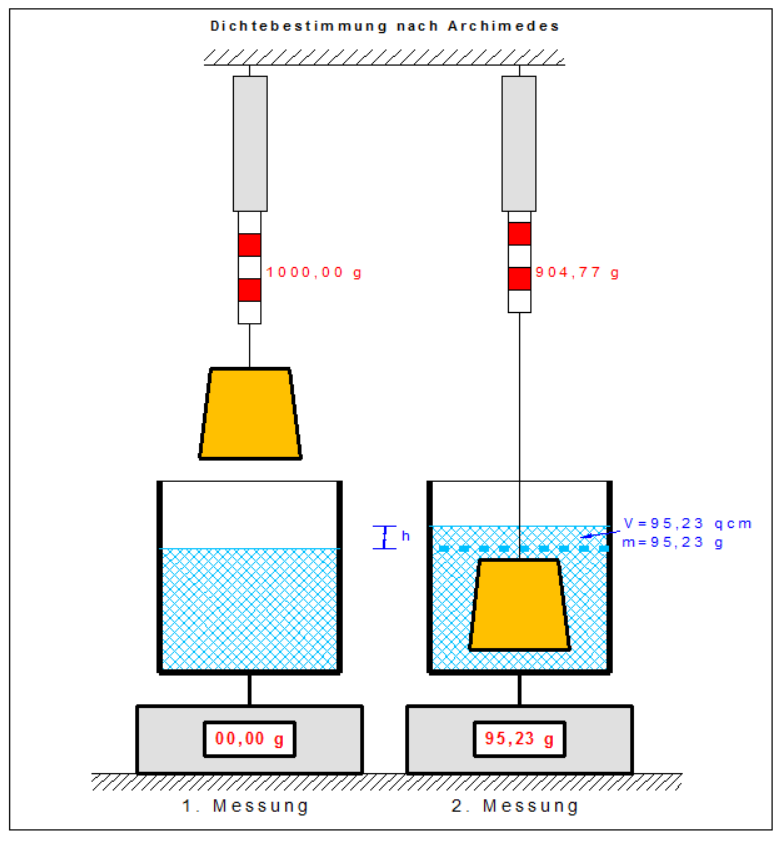
Anhand der Zeichnung soll das Prinzip der Dichtebestimmung eines gelb dargestellten Edelmetallkörpers erklärt werden. Zwar werden aus didaktischen Gründen vier Waagen dargestellt, man wird aber sehen, dass 2 Wägungen reichen. Auf der linken Seite wird die Masse des Edelmetallkörpers an Luft bestimmt. Ergebnis an der oberen Waage: 1000g. Der Wasserbehälter darunter steht auf einer Waage die auf den Wert 0 tariert wurde. Nun wird der Edelmetallkörper vollständig in das Wasser eingetaucht, wodurch er so viel Wasser verdrängt, wie der Körper Volumen hat. Der Wasserspiegel wird deshalb um den Wert h ansteigen, so als ob man Wasser bis zu der neuen Füllstandshöhe zugefüllt hätte. Diese fiktive Zunahme an Wasser wirkt sich auf der unteren Waage in einer Massenzunahme (=“Gewichtszunahme“) von hier 95,23 g aus. Die fiktive Wasserzunahme beträgt also m=95,23 g und das entspricht einer Volumenzunahme von V=95,23 qcm.
Die obere Waage zeigt nach dem Eintauchen ein um eben diese 95,23 g reduziertes Gewicht an, da ja der Edelmetallkörper im Wasser einen Auftrieb erfährt. Zu beachten ist, dass die Summe der Messwerte der beiden Waagen jeweils vor und nach dem Eintauchen gleich sind, da die Masse des Körpers unverändert ist.
Wenn man die Dichte des Formkörpers berechnen will, benötigt man die untere Waage nicht. Alle Informationen sind in den zwei Messungen an der oberen Waage ablesbar, denn die Differenz der beiden Messungen ergibt das Volumen V des Körpers. Bei unserem Beispiel ergibt sich für die Dichte ρ:
ρ=“Masse an Luft“ / „Volumen“ = 1000/(1000-904,77) = 1000/95,23 = 10,50 (g/qcm) . Das ist die Dichte von Silber!
(Hinweis: Wenn man ganz präzise Labormessungen zur Dichtebestimmung durchführt, muss man auch noch den Auftrieb in Luft und die Temperatur der Medien Luft und Wasser berücksichtigen. Bei der Genauigkeit der hier verwendeten Waagen ist das aber nicht sinnvoll!)
Durch die Dichtebestimmung kann man nicht nur das Element der Probe sondern auch die Legierung analysieren, da das spezifische Gewicht z.B. der verschiedenen Goldlegierungen bekannt ist:
999 (24 Karat) = 19,3 g/qcm
900 (21 Karat) = 17,5 g/qcm
750 (18 Karat) = 15,1-15,8 g/qcm (je nach Zusammensetzung der Legierung)
585 (14 Karat) = 13,1-13,6 g/qcm (je nach Zusammensetzung der Legierung)
375 (9 Karat) = ca. 11, g/qcm (je nach Zusammensetzung der Legierung)
333 (8 Karat) = 10,5-10,9 g/qcm (je nach Zusammensetzung der Legierung)